Latihan Mengintegrasikan Video dari Youtube ke Blog

 

Klik link dibawah ini

Video Trip Codetan Kali Comal

POLA BILANGAN 2 (Menentukan Suku Ke-n)

Assalamu'alaikum Wr. Wb.

Anak-anak pada minggu kemarin kita telah belajar bersama menentukan suku berikutnya dari suatu pola bilangan. Alhamdulillah kalian sudah cukup menguasi mater itu terbukti dengan nilai kalian dalam mengerjakan soal Quizizz rata-rata sudah cukup baik.

Pada minggu ini kita akan belajar bersama Menentukan Suku Ke-n dari suatu Pola Bilangan.

Untuk lebih memahami cara menentukan suku ke-n dari suatu Pola Bilangan, mari sekali lagi kita cermati video tutorial berikut dengan seksama

Nah mudah kan?

Untuk mengetahui pemahaman kalian tentang materi diatas kerjakan soal-soal berikut dengan cara klik

http://gg.gg/Soal-Pola-Bilangan-2

Selamat Mengerjakan Semoga Sukses

Aamiin

BILANGAN BULAT

Assalamu alaikum Wr. Wb.

Anak-anak sebelum memulai pelajaran, bapak akan memperkenalkan diri dulu

 

Nama         : Taroso, S.Pd.

Alamat       : Desa Penggarit Rt. 02 Rw.02 Kecamatan Taman

Mengajar   : Matematika

Keluarga

Baiklah, mari kita mulai pelajaran yang pertama tentang:

Pengertian Bilangan Bulat

Setiap berbicara tentang mata pelajaran Matematika, kamu pasti seringkali mendengar kata bilangan 'kan?. Bilangan dapat diartikan menghitung (membilang). Dari sini, kita jadi tahu betapa pentingnya bilangan dalam ilmu matematika bukan? Nah, berikut ini kita akan membahas tentang pengertian dan contoh bilangan bulat. Apa sih bilangan bulat itu? Yuk, kita simak.

Dari skema di atas, dapat dilihat bahwa bilangan bulat termasuk bilangan rasional yang merupakan bagian dari bilangan real. Selain itu, bilangan bulat terdiri dari:

1. Bilangan bulat negatif = {...,–5,–4,–3,–2,–1}
2. Bilangan nol = {0}
3. Bilangan asli atau bilangan bulat positif = {1,2,3,4,5,...} yang dapat terbagi menjadi:
1. Bilangan ganjil = {1,3,5,7,...}
2. Bilangan genap = {2,4,6,8,...}

Bilangan nol dan bilangan asli membentuk bilangan yang disebut : 

                  Bilangan cacah = {0,1,2,3,...}

Urutan Pada Bilangan Bulat

Untuk memahami urutan pada bilangan bulat, mari kita simak Video berikut ini dengan cara klik tanda panah

Nah mudah kan?

Untuk memantapkan pemahaman kalian mari kita kerjakan kuis berikut ini dengan cara klik

 Soal Urutan Bilangan Bulat 

( sebelum mulai mengerjakan jangan lupa tulis nama dan kelas kalian, contoh: Budi Prakoso 7B )

SELAMAT MENGERJAKAN SEMOGA SUKSES

AAMIIN

POLA BILANGAN

Untuk memahami Pola Bilangan perhatikan video berikut ini ( klik tanda panah untuk menonton )

Setelah nonton video, sekarang coba kerjakan soal berikut dengan cara klik Soal Pola Bilangan (1)

jangan lupa tulis nana dan kelas sebelum jawab Quizizz

SELAMAT MENGERJAKAN SEMOGA SUKSES

AAMIIN

Kumpulan Soal PTS Gasal Matematika Kelas 7

Silahkan kerjakan soal dibawah ini dengan cara klik link di bawah ini

1. Uji Kompetensi Bilangan

2. Himpunan

3. Bentuk Aljabar

Selamat mengerjakan semoga sukses... Aamiin

Teorema Pythagoras

Teorema Phytagoras

Teorema Phytagoras merupakan seuah aturan matematika yang bisa dipakai dalam menentukan panjang salah satu sisi dari suatu segitiga siku-siku.

Yang perlu kalian ingat dari teorema ini yaitu teorema hanya berlaku untuk segitiga siku-siku. Maka dari itu tidak dapat digunakan untuk menentukan sisi dari sebuah segitiga lain yang tidak berbentuk siku-siku.

Teorema pythagoras masuk ke dalam salah satu materi dalam mata pelajaran matematika dasar yang mempunyai perluasan serta manfaat yang sangat banyak.

Materi ini juga sangat banyak dimanfaatkan serta sangat sering keluar dalam soal-soal ujian nasional.

Pada dasarnya, teorema pythagoras sangatlah sederhana yakni kita hanya diminta untuk menghitung panjang sisi dari suatu segitiga siku-siku di mana sisi lainnya telah kita ketahui.

Sifat Teorema Pythagoras

Terdapat dua sifat yang ada dalam teorema pythagoras,  diantaranya yaitu:

1. Hanya untuk segitiga siku-siku
2. Minimal 2 sisinya dapat diketahui terlebih dahulu

Permasalahan lain yang sering dijumpai yaitu dalam mengidentifikasi suatu segitiga siku-siku.

Bagian mana sisi miringnya, serta sisi lainnya. Untuk itu akan kami berikan sebuah segitiga siku-siku serta mengajak kalian untuk memahami setiap komponen dari segi tiga siku-siku.

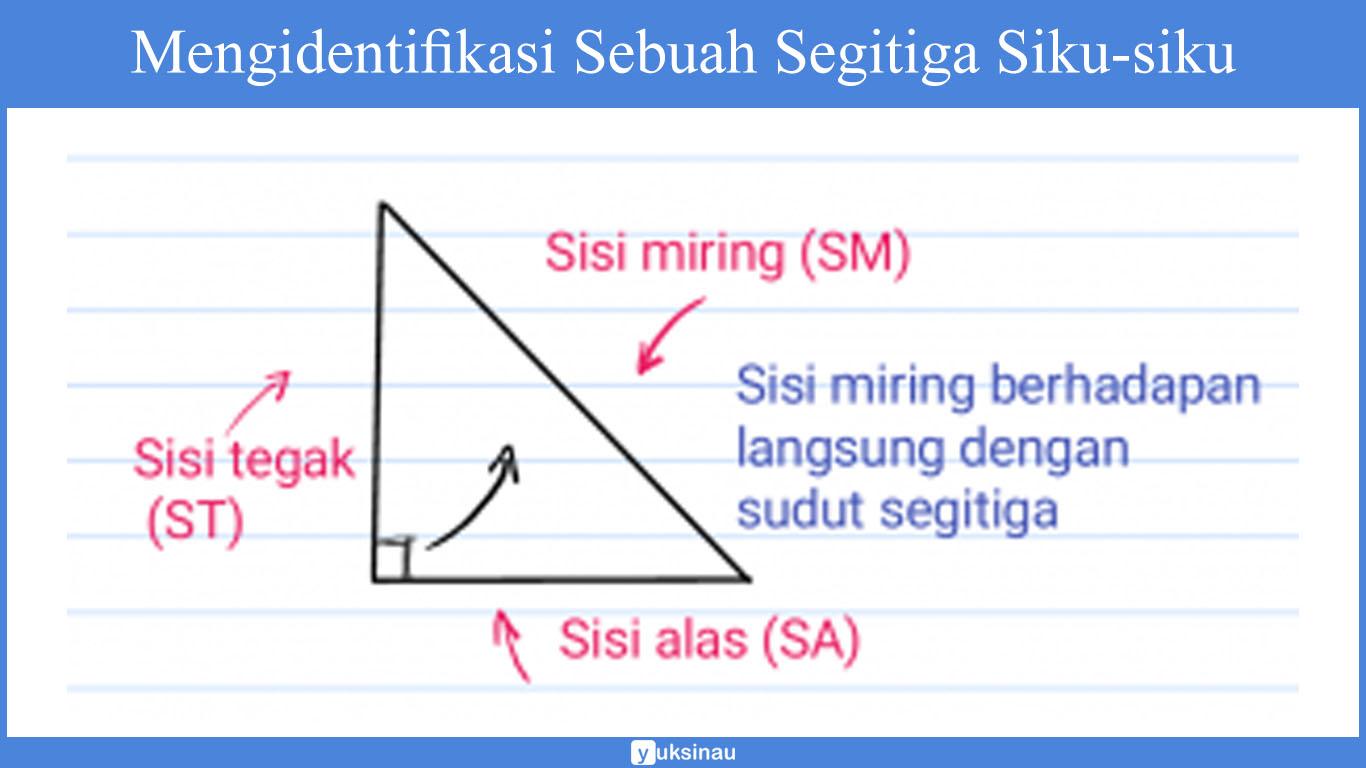
Dalam gambar di atas bisa kita jumpai jika sisi miring berada tepat di depan siku-siku dari sebuah segitiga tersebut.

Siku-siku pada umumnya digambarkan dengan sebuah kotak kecil di dalamnya, seperti gambar di atas yang ditunjuk dengan panah hitam.

Sisi miring tersebut berhadapan langsung dengan sudut siku-siku dari segi tiga di atas. Untuk sisi alas dan juga sisi tegaknya sebenarnya tidak terlalu bermasalah jika kalian keliru dalam mengidentifikasi nya.

Mengapa kalian butuh untuk memperhatikan dan memahami bentuk sebuah segitiga siku-siku?

Karena, agar jika kalian menjumpai segitiga siku-siku nya di balik atau diganti namanya kalian tidak akan mengalami kesuliatan.

Itulah mengapa kalian butuh untuk memahami sekaligus mengidentifikasi suatu segitiga siku-siku.

Sebagai contoh, perhatikan baik-baik gambar di bawah ini:

Walaupun segitiga siku-siku tersebut sudah kita balik, kalian telah mampu mengidentifikasi sisi miring, sisi alas, dan sisi tegaknya.

Pada gambar di atas sisi miring yaitu sisi r, sisi alasnya yaitu sisi p, serta sisi tegaknya yaitu sisi q.

Rumus Teorema Pythagoras

Rumus Phytagoras merupakan rumus yang diperoleh dari materi Teorema Phytagoras.

Teorema Phytagoras sendiri seperti yang telah dissebutkan di atas merupakan teorema yang menerangkan tentang hubungan antara sisi-sisi yang ada dalam sebuah segitiga siku-siku.

Teorema ini pertama kali dikemukakan oleh seorang matematikiawan yang berasal dari Yunani bernama Phytagoras.

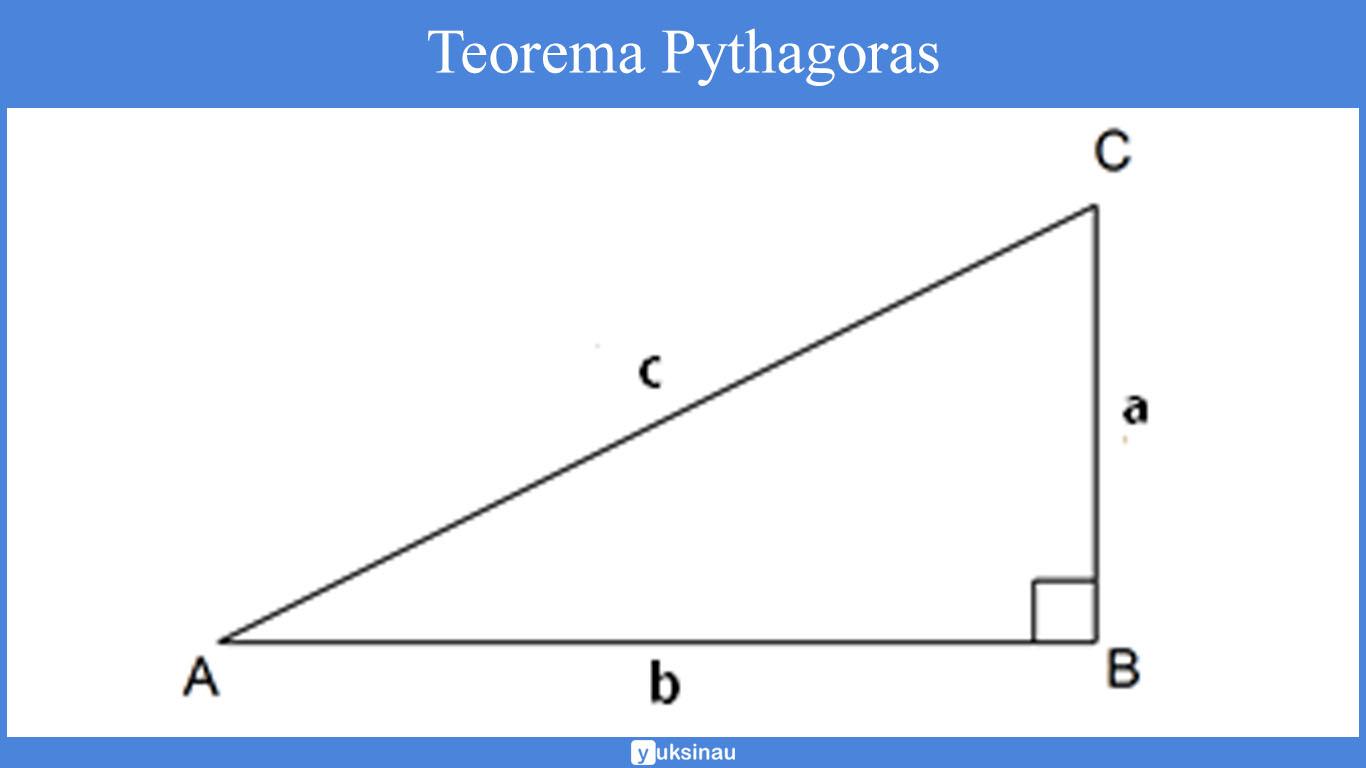
Sebagai contoh, diketahui sebuah segitiga dengan siku-siku di B. Apabila panjang sisi miring (hipotenusa) yaitu c serta panjang sisi-sisi penyikunya (sisi selain sisi miring) yaitu a dan b. Maka teorema Phytagoras di atas bisa kita rumuskan seperti berikut ini:

Rumus Phytagoras

c² = a²  + b²

Keterangan:

c = sisi miring
a = tinggi
b = alas

Rumus Phytagoras pada umumnya dipakai dalam mencari panjang sisi miring segitiga siku-siku seperti berikut ini:

Kuadrat sisi AC = kuadrat sisi AB + kuadrat sisi BC. atau AC² = AB² + BC²

Rumus untuk mencari panjang sisi alas yaitu:

b² = c²  – a²

Rumus untuk mencari sisi samping atau tinggi segitiga yaitu:

a² = c²  – b²

Rumus untuk mencari sisi miring segitiga siku-siku yaitu:

c² = a²  + b²

Contoh Soal Pythagoras (Pitagoras) dan Penyelesaiannya

Soal 1.

Diketahui segitiga siku-siku ABC dengan siku-siku di B yang digambarkan sebagai berikut:

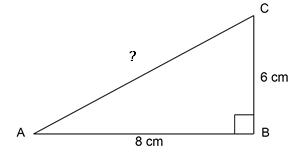
entukan panjang sisi miring AC pada gambar di atas!

Jawab:

Sebab segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti betikut ini:

AC² = AB² + BC²
AC² = 8² + 6²
AC² = 64 + 36
AC² = 100
AC  =  √100
AC  = 10

Sehingga, panjang sisi AC dalam segitiga siku-siku tersebut yaitu 10 cm.

Soal 2.

Suatu segitiga siku-siku KLM dengan siku-siku di L digambarkan seperti di bawah ini:

Tentukan panjang sisi KL pada gambar di atas!

Jawab:

Sebab, segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti berikut ini:

KM² = KL² + LM²
KL² = KM² – LM²
KL² = 13² – 12²
KL² = 169 – 144
KL² = 25
KL  =  √25
KL = 5

Sehingga, panjang sisi KL dalam segitiga siku-siku di atas yaitu 5 cm.

UJI KOMPETENSI

Silahkan klik link dibawah ini untuk mengerjakan

SOAL TEOREMA PYTHAGORAS

Selamat mengerjakan semoga sukses

Biodata Penulis

Nama    : Taroso, S.Pd.

Instansi    : SMP Negeri 1 Taman